A library’s readme is a means to understand what it can do, not how it was made. This is practical, but also a shame - open source libraries constitute a huge body of (mostly) idiomatic code by (mostly) experienced practitioners that can be learned from.
This post, which I intend to be the first in a series, will discuss the design considerations and implementation details of Rhizome, a library for graph and tree visualization. It will discuss the reasons behind certain design choices, and cherry-pick interesting parts of the codebase for in-depth exploration.
Few, if any, of these design choices are objectively correct. Rather, they are a result of my own tastes and what seemed right in the moment. Attempts to extract general truths about software or Clojure from these posts will end in tears.
other posts in this series
representing trees and graphs as data
Representing a tree structure using Clojure data structures is very straightforward, but there are a variety of approaches we can use. Take this simple example:
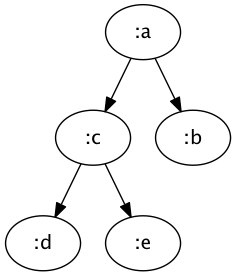
A simple but somewhat verbose representation is via maps that contains lists of child maps:
{:node :a
:children [{:node :b}
{:node :c
:children [{:node :d}
{:node :e}]}]}
Using Clojure’s tree-seq function, we can do a pre-order traversal of the structure. tree-seq takes two functions in addition to the structure itself, branch? and children. branch? should return a falsey value if the node is a leaf, and a truthy value otherwise. children should return a sequence of the node’s children, and will only be invoked if branch? is true. Oftentimes, these functions are the same; in our case :children will return the sequence of children, and nil if there are no children.
> (tree-seq :children :children list-of-maps)
({:node :a
:children [{:node :b}
{:node :c, :children [{:node :d} {:node :e}]}]}
{:node :b}
{:node :c, :children [{:node :d} {:node :e}]}
{:node :d}
{:node :e})
Note that the first element of this list is entire structure, followed by sub-structures representing the children. But since we’ve also included a :node key that identifies each node, this traversal can be more easily understood by only looking at that value:
> (map :node (tree-seq :children :children list-of-maps))
(:a :b :c :d :e)
A more compact representation is possible, though:
{:a {:b nil
:c {:d nil
:e nil}}}
This treats each node as a map entry, where the key is the node name, and the value is the children. This is only a valid representation if siblings have unique identifiers; in the previous representation we could have multiple nodes with the same name. Again, in this case a single function, val, can be used for both branch? and children.
However, this won’t work:
> (tree-seq val val map-of-maps)
ClassCastException
This is because we’ve defined our nodes to be map entries, but our top-most node is a map. Since our structure is non-uniform, we can either make the structure uniform, or modify the functions to handle a non-uniform structure:
(tree-seq val val (first map-of-maps))
(tree-seq
#(or (map? %) (val %))
#(if (map? %) (val (first %)) (val %)
map-of-maps)
In this case, the former is clearly simpler, but this will vary depending on how your tree is represented.
tree-seq uniquely identifies nodes by their path from the root of the tree. However, in a graph nodes may be accessible via multiple paths from the root.
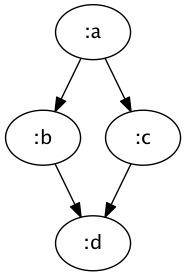
To represent :d positionally, we need to duplicate it beneath both :b and :c.
{:a {:b {:d nil}
:c {:d nil}}}
This will work, but in larger graph structures this can greatly increase the size of both the serialized and in-memory representation. It only works, however, because the previous example doesn’t have a cycle.
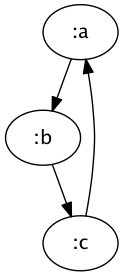
{:a {:b {:c ?}}}
Using mutable references, we could create a pointer to the enclosing data structure, but an immutable data structure cannot represent cycles positionally. Instead, we need to use unique identifiers for each node:
{:a [:b]
:b [:c]
:c [:a]}
This is a map of nodes onto adjacent nodes. There’s no concept of a root, so there’s no reference point from which to position other nodes. Rather, to identify a node we need a unique identifier, but as long as we can guarantee such an identifier exists, we can represent arbitrary graph structures. Since Rhizome is designed to represent arbitrary graphs, it assumes nodes are identified by identity rather than position.
In Rhizome, a graph is represented by two values: a list of nodes, and a function that takes a node and returns a list of adjacent nodes. For the above map, these would be the keys of the map, and the map itself, respectively. For tree structures, where it can unambiguously reference nodes positionally, it mimics tree-seq.
interfacing with graphviz
Graph layout is a difficult problem, but it’s not the one Rhizome is trying to solve. Luckily, a tool exists which solves this for us. Unluckily, it’s not a Java library, it’s a command-line tool. This means that it can’t be implicitly installed via Maven dependencies, and it also means that we can’t use a programmatic API. Instead, we have to use the DOT language.
Graphviz is not designed to be a compilation target, it’s optimized for being a human readable specification for graphs. The simplest version of our three-node loop would look like this:
digraph {
a -> b;
b -> c;
c -> a;
}
or simply
digraph {
a -> b -> c -> a;
}
We can also explicitly declare the nodes before describing the edges between them, and separate the node identifier from its presentation.
digraph {
node1[label=a];
node2[label=b];
node3[label=c];
node1 -> node2;
node2 -> node3;
node3 -> node1;
}
This format makes the same basic assumption as above: a node’s identifier and its identity are equivalent. Since in Rhizome the nodes can be any object with .equals implemented, in order to be able to create a DOT representation of our data we need a mapping of objects onto identifiers. Luckily, this is easily accomplished:
(memoize
(fn [_]
(gensym "node")))
This creates a memoized version of a function which ignores the input, and creates a unique symbol of the form node123 via gensym. By memoizing this function, we ensure that we will only call gensym once per unique object, thus creating our mapping.
Note that memoization can be an extremely dangerous technique to use, especially in a library. It will create a permanent reference to both the parameters and results for each unique set of parameters, which means that if the parameters aren’t bounded, neither is the memory usage. The only way this is safe is if we know the parameters are bounded, or the lifetime of the memoized function is bounded.
In a library, it’s very hard to make guarantees about what inputs we’ll be given, but at least in this case we can guarantee the lifetime of the function, by defining it in a let scope:
(let [node->identifier (memoize (fn [_] (gensym "node")))]
...)
Within this context, we can call node->identifier with any inputs we like, because the memoized function can be collected the moment we leave the scope. Thus, we can call:
> (def g
{:a [:b :c]
:b [:c]
:c [:a]})
#'g
> (view-graph (keys g) g
:node->descriptor (fn [n] {:label n}))
which yields the following DOT descriptor:
digraph {
node1303[label=":a"]
node1304[label=":c"]
node1305[label=":b"]
node1303 -> node1305[label=""]
node1303 -> node1304[label=""]
node1304 -> node1303[label=""]
node1305 -> node1304[label=""]
}
and, when we shell out to GraphViz’s command line tool dot with this string, we get this image:
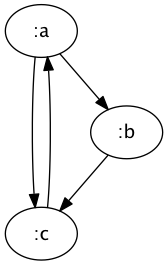
But unfortunately, it’s not quite that simple. GraphViz allows nodes to be clustered together:
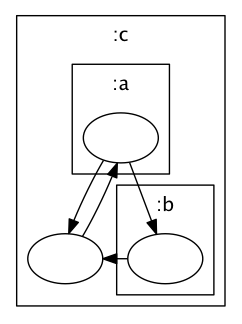
This is described by subgraph entries in the DOT descriptor:
digraph {
subgraph cluster1332 {
graph[dpi=100, rankdir=TP, label=":c"]
node1333[label=""]
subgraph cluster1334 {
graph[dpi=100, rankdir=TP, label=":a"]
node1335[label=""]
}
subgraph cluster1336 {
graph[dpi=100, rankdir=TP, label=":b"]
node1337[label=""]
}
}
node1335 -> node1337[label=""]
node1335 -> node1333[label=""]
node1333 -> node1335[label=""]
node1337 -> node1333[label=""]
}
Each of these sub-clauses is very similar to the parent structures, and can be arbitrarily nested. As such, it is most easily constructed with a recursive function. However, Clojure’s let bindings are lexical, and don’t extend into recursive calls. We could make the memoized gensym call a parameter, but since we also need a separate generator for cluster names, we can make our parameter list much simpler by just using Clojure’s dynamic binding capabilities.
(def ^:private ^:dynamic *node->id* nil)
(def ^:private ^:dynamic *cluster->id* nil)
(defn- node->id [n]
(*node->id* n))
(defn- cluster->id [s]
(*cluster->id* s))
(defmacro ^:private with-gensyms
[& body]
`(binding [*node->id*
(or *node->id*
(memoize (fn [_#] (gensym "node"))))
*cluster->id*
(or *cluster->id*
(memoize (fn [_#] (gensym "cluster"))))]
~@body))
Here, we define two vars, which within the scope of with-gensyms will hold the memoized functions. Since these vars are an implementation detail, we interact with them via the node->id and cluster->id functions. This isn’t strictly necessary, but it leaves the door open for validation, better error messages, and other nice affordances. Generally, there should always be a function between thread-local vars and other code.
Finally, in with-gensyms we define thread-local values for the two vars, but first check if they’re already non-nil, in which case we simply pass the old value through. This means that the memoized functions are only created once, and then propagated down the call stack. Like the let binding, once we exit the outermost scope, the functions are free to be collected.
Graphviz assumes explicit identities for nodes, so what about when we want to represent a tree? We can’t simply use the identity of the node, because the same value at different positions within the tree must be treated as separate nodes. One possibility is to represent each node as a tuple of its value and its position in the tree, but this forces us to consider how to represent positions, which is neither obvious nor straightforward.
Luckily, there’s a better way.
(let [node->children (atom {})
nodes (tree-seq
(comp branch? second)
(fn [x]
(swap! node->children assoc x
(map vector
(repeatedly #(Object.))
(children (second x))))
(@node->children x))
[(Object.) root])]
...)
If we’re given the tree-seq parameters of root, branch? and children, we can simply walk the structure, and transform each node into a unique version of itself. Since tree-seq only visits each node once, we don’t need a reproducible unique value, we can simply create a tuple of the value and (Object.), which creates an instance of the base class for all Java objects. This instance doesn’t do much, but it does have a nice property: it’s only equal to itself. Thus, the tuple we create with this object is unique no matter how many nodes share the same value. By flattening the tree using tree-seq, we have a list of nodes, and a function that gives adjacent nodes via #(@node->children %).
Rhizome attempts to be REPL-friendly by moving the window displaying the rendered graph above every other window whenever the image is updated. Unfortunately, this is extremely difficult to do in a cross-platform way. The Swing JFrame has a method called .setAlwaysOnTop which, by all rights, should do exactly what you’d expect, so all you’d need was something like:
(doto frame
(.setAlwaysOnTop true)
(.setAlwaysOnTop false)))
Unfortunately, this isn’t always sufficient, so the standard incantation looks more like this:
(doto frame
(.setExtendedState JFrame/NORMAL)
(.setAlwaysOnTop true)
.repaint
.toFront
.requestFocus
(.setAlwaysOnTop false))
Even then, however, in more recent versions of OS X this doesn’t do the trick. So for that environment, we’re forced to do something rather special:
(defn- send-to-front
"Makes absolutely, completely sure that the frame
is moved to the front."
[^JFrame frame]
(doto frame
(.setExtendedState JFrame/NORMAL)
(.setAlwaysOnTop true)
.repaint
.toFront
.requestFocus
(.setAlwaysOnTop false))
;; may I one day be forgiven
(when-let [applescript (.getEngineByName
(ScriptEngineManager.)
"AppleScript")]
(try
(.eval applescript "tell me to activate")
(catch Throwable e
))))
Write it once, they said. Run it anywhere, they said.